Have you ever heard of the term "bijection"? A bijection is a comparison of two sets of things without actually counting them. This sounds incredibly confusing, but it is actually very simple. Here is an example:
{1,3,5,7,9} and {2,4,6,8,10}
Here we have two sets that both have five numbers in them. If you place the sets over each other like this:
{1, 3, 5, 7, 9}
{2, 4, 6, 8, 10}
It is easy to see the bijection. You can just draw a line from 1 to 2, 3 to 4, 5 to 6, 7 to 8, and 9 to 10.

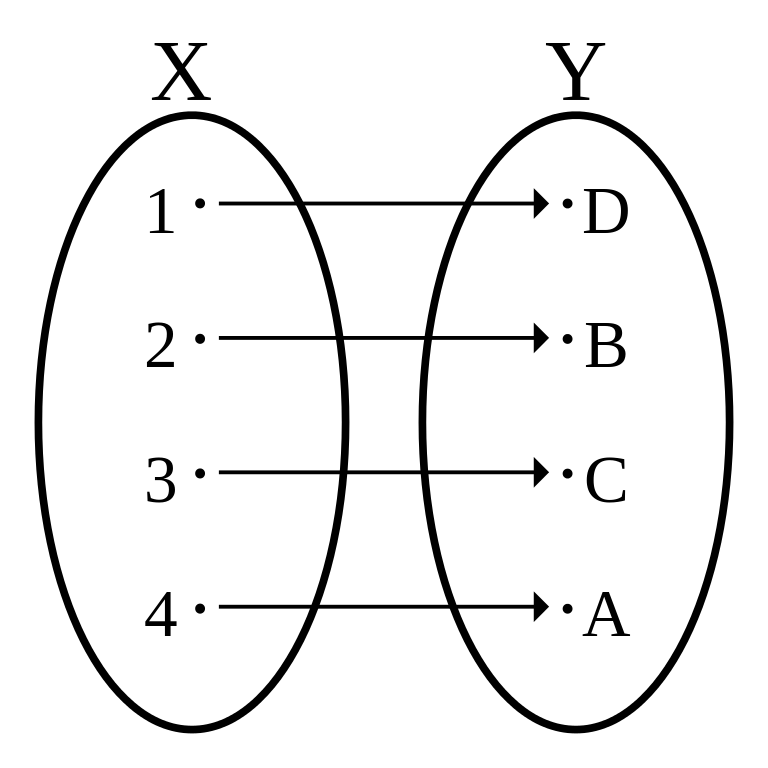
The example on the right is also a bijection

There are 3 requirements for a bijection to be a bijection:

1. Every number in the first set corresponds with a single number in the second set
2. Every number in the second set corresponds with a single number in the first set
3. Every number is used once and only once

Now, what if we had larger sets? Such as {1, 3, 5, ... 99} and {2, 4, 6, ... 100}? We can still make a bijection using the same method we used for the first example. Draw a line from each number in the first set to each number 1 greater than it in the second. This way, every single number is used in both sets, no number is used more than once, so we deduce that these sets are equal.

Now, what would happen if we had sets that went on forever? Can we still make bijections with those? The answer is yes. Because infinities are so large, and cannot be counted, we rely on bijections to compare the sizes of different infinities. I will show some startling discovers that will blow your mind on the next page.