Proofs that Seem to Defy Mathematics
Here is a couple of proofs that seem to "defy" mathematics, by proving things that are obviously not true. I challenge you to try and find the mistake in all proofs, before looking at the answers down at the bottom of the page. I do not take credit for any of these. I hope you enjoy these as much as I did!
pi = 2
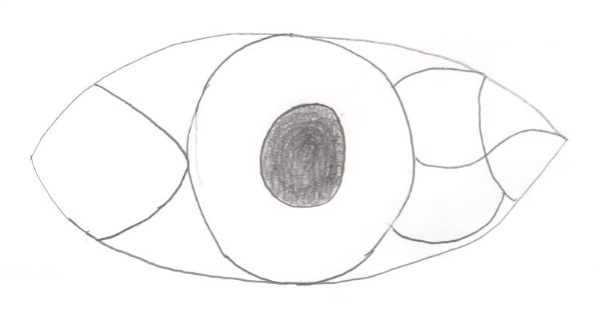
The first proof is the proof that pi is equal to 2. Take the picture found on the right. It is a circle with a diameter of 2. There are many half circles of different sizes found along the diameter. The proof is as follows:
The diameter of this circle is 2. The formula for circumference is c = (pi)(d), or in this case, 2 pi. Because the circumference is two pi, then half the circumference of the circle is pi. In summary, the distance from one end of the diameter to the other, following the circumference, is pi.
Now look at the black line in the middle of the circle. This is two half circles placed along the diameter of the large circle. One half of the diameter is 1, so each circle has a diameter of 1. The circumference of each of these circles is pi. Because each is a half circle, pi/2 + pi/2 = pi, the length of the black line. Note that this is the same length as half the circumference of the big circle.
Now look at the red line. Instead of two half circles, we now have four half circles. The diameter for each of these circles is ½. The circumference of an entire circle this size would be pi/2, but because they are only half circumferences, the length is pi/4. Add the four lengths of pi/4 together, and you get pi again.
Now look at the green line. We have the same situations, but now, following the same procedure, we have 8 pi/8 segments. This totals to pi again. Keep doing this for pi/16, pi/32, etc. and you come to the conclusion that as the pi lines get smaller, they eventually reach 2. Therefore, pi = 2.
2 = 1
This next proof is the proof that 2 is equal to 1. It is relatively simple compared to the previously problem.
a = b
a^2 = ab
a^2 + a^2 = a^2 + ab
2a^2 = a^2 + ab
2a^2 − 2ab = a^2 + ab − 2ab
2a^2 − 2ab = a^2 − ab
2(a^2 − ab) = 1(a^2 − ab)
2 = 1
Relatively simple, right?!
-1 = 1
I saved my favorite proof for last: the proof that -1 is equal to one. This proof uses the imaginary number i. i is the square root of a negative 1, and i squared is a negative 1. The proof that -1 is equal to 1 is as follows:
i = √-1
i^2 = (√-1)(√-1)
i^2 = √((-1)(-1))
-1 = √1
-1 = 1
This is the hardest "proof" to find the fallacy. Again, try to find the mistake yourself first, and then scroll down to the bottom to discover.
In the first problem, no matter how small the line gets, it will always keep its curve: it will never actually be the same as the straight line.
In the second problem, the second to last step is 2(a^2 − ab) = 1(a^2 − ab). However, remember the second step: a^2 = ab. Because a^2 = ab, a^2 - ab = 0. So yes, 2(0) is equal to 1(0), but you cannot divide by 0 to get that 2 = 1.
In the last problem, when you take the square root, the answer must be plus OR minus. So the square root of 1 is plus or minus one. This is equal to -1.

